期末考试前和昍谈起数学解题中的验算，他说他的验算方法很简单，就是重做一遍。这成为了我写这篇文章的动机。

       重做一遍确实是许多人验算的第一选择，但这是最笨的一种做法。由于惯性思维的存在，重做一遍不仅耗时耗力，还可能会导致两次踏进同一条河流。验算，其实需要高超的技巧和敏锐的洞察力。今天，我就想从我自己以前做数学题的经验谈谈怎样做好验算。后面是纯干货，请静下心来和小朋友一起看。

（1）    换一种计算方法

    刚学计算的孩子很多都苦恼为什么孩子又算错了。计算题的验算，通常是再算一遍，但不是傻傻的重算一遍，最好是换一种方式再算一遍。    

    怎么换一种方式？    

    常用的有逆运算法。即加法用减法再算一遍，除法则用乘法再算一遍。比如112-43=69， 可以通过43+69=112来验算。

    而对于综合算式，可以充分运用交换律、结合律和分配律等改变运算顺序再算一次。

    比如35×48，可以再用48×35再算一遍，或者变成35×50-35×2算一遍；

    比如135+43-55，可以变成135-55+43重新算一遍。

    对于应用题，另寻一种解法也是我必用的一种验算方法。

    例：明明家距离上海世博园1950米。周末，他与妈妈8:00出发，步行到世博园去玩，8:20时他们距离世博园还有650米，照这样计算，他们还需要走多少分钟才能到达世博园？

    正常解法： 20分钟走了1950-650=1300米，所以速度是1300÷20=65米/分。还需要走650÷65=10分钟

    验算解法1： 同解法1求出速度65米/分，总时间需要1950÷65=30分，还需要走30-20=10分钟

    验算解法2：20分钟走了1300米，还剩下650米，由于1300÷650=2，所以剩下的路程需要走已经走的一半时间，即10分钟。

    再譬如经典的鸡兔同笼问题：鸡、兔同笼，上有35头，下有94足，问鸡兔多少只？

    假如采用假设法解题。假设全是鸡，那么有70只脚，但实际多了94-70=24只脚。而如果将1鸡换成1只兔，那么就多2只脚，因此应该把24÷2=12只鸡换成兔，因此共有12只兔，23只鸡。

    验算时，就千万不要再假设全是鸡了，可以假设全是兔。那么应该有35×4=140只脚，实际少了46脚。把一只兔子换成一只鸡，少2只脚，因此应该把4÷2=23只兔换成鸡，这就得到了和上面相同的答案。

（2）    代入验算法

代入验算，顾名思义，就是把结果代入未知量，如果符合给出的条件，则答案就是正确的。小学数学比较难的是做逆向思考，这种问题其实在学过方程后就变得很简单，也最适合用代入验算法。

比如上面的鸡兔同笼问题的验算，最直接的验算法就是代入验算。12只鸡和23只兔对不对呢？那只需要算一下一共有多少个头和脚。头的总数是12+23=35，脚的总数是12×4+23×2=94只，符合条件，因此正确。

再看另一个题：小明步行去电影院，如果每分钟走45米，则迟到一分钟，如果每分钟走50米则早到一分钟。请问小明家到电影院相距多少米？

一种做法是假设有两个小明同时走，一个走的快，一个走的慢。那么，如果在电影正常开始的时候，快的小明已经超过了电影院50米，而慢的小明则还距离电影院45米。此时，慢的小明落后快的小明95米。因此，总共走了95÷（50-45）=19分。

此时，慢的小明走了19×45米，家到电影院的距离就是19×45+1×45=900米。

900米到底对不对，我们可以代入验算一下。如果家到电影院距离900米，那么以50米/分需要900÷50=18分，比计划时间早1分钟，所以正常是19分钟。如果以45米/分走，那么19分钟可以走45×19，还需要走（900-45×19）÷45=1分，满足条件。

（3）    小规模实验验证法

对于一个规模较大的问题，当找出了规律但无法百分百确定时，可以用小规模的数量进行实验进行确认。

刚学等差数列的孩子，最难的是计算项数，比如：2，5，8，11, ….2018 这个数列一共有多少项？

喜欢背公式的孩子常常不太确定项数到底是(a_n-a₁)/d还是(a_n-a₁)/d+1时，就可以使用小规模实验验证方法来验证一下。比如，就取3项，那么（8-2）/3=2，因此应该是(a_n-a₁)/d+1。

当然，理解这个问题的最好的办法是用栽树的做法类比。小朋友们都知道这样的题：在一条长100米的水渠边每隔5米栽一棵树，那么一共可以栽多少棵树？  答案是100÷5+1。

对应到上面的等差数列，2018-2=2016就是水渠的长度，每个数列的元素就是一棵树，每棵树之间隔3米，因此求数列的项数就转变为求栽树的棵数，为2016÷3+1.

又比如下面这个公倍数的题：按下面的规律排列，请问第10次出现“我E“的是第几列？

通过观察，我们发现上面一行的周期是4，下面一行的周期是6。因此整个重复的周期是12。第一次出现“我E“是第5列，那么第10次应该是5+（10-1）×12=113。

验算我们不可能列出那么多列，但总结出的规律是出现“我E“的列数应该除以12余5。那么可以画到17列，以验证这一假设。

（4）    极端/特殊取值验证法

有些时候，通过一般性的解法解得了一个答案后，可以用特殊/极端取值对答案进行验证。其原理很简单，既然在所有情况都成立，那么在一些特殊取值下也要成立。

例如，下图中，O是边长为2厘米的正方形的中心，∠POQ为直角，求阴影部分的面积。

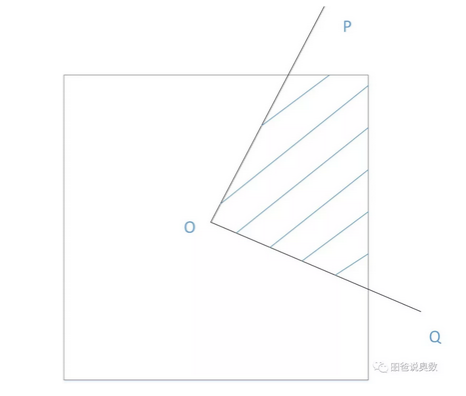
花了不少时间算出来了面积是1平方厘米（至于怎么算，这里就不多说了），那么到底对不对呢？可以假设一种极端情况，即∠POQ的两条直角边和正方形的边分别垂直，那此时阴影部分的面积就是1平方厘米。

又如：上下同一个坡，上坡6米/秒，下坡12米/秒，求上下坡的平均速度？

一般化的解法是把坡长度看成1，那么上坡时间1/6，下坡时间1/12，因此平均速度为2÷(1/6+1/12)=8米/秒。

对不对？可以假设坡长为一个特殊的值，如24米，那么上坡4分钟，下坡2分钟，平均速度就是24×2÷(4+2)=8米/秒。

（5）    估算法

估算可以花很少的代价来发现一些明显的错误，但不能保证发现所有的错误。取值的范围，一些常识和奇偶性等，都可以用于辅助验算。

例如：10年前妈妈的年龄是儿子年龄的7倍，15年后妈妈的年龄是儿子的2倍，问今年妈妈和儿子各多少岁？

妈妈和儿子的年龄总得差个20来岁，但也不能超过50岁，这算是基本常识。因此，如果算出来妈妈和儿子的年龄分别是30岁和18岁，那大概就错了。

奇偶性可以辅助发现计算题中的错误。比如 1187÷34=

如果算出来答案是31…16, 那就肯定不对了，因为余数应该是个奇数，偶数肯定就错了。

今天就想到这些，欢迎大家补充。