打小我们就和立方体打交道，可以说它是我们最熟悉的一种空间几何形状了。但立方体中的学问，你真的都懂了吗？

1. 相对面和相邻面

先看一个我们小学练习中经常会出现的问题：

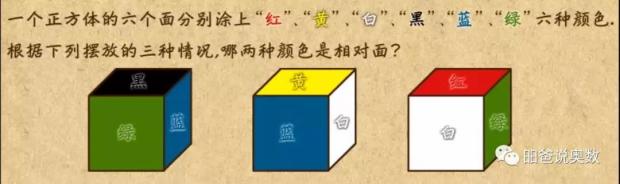
首先我们有下面的最基本常识：正方体中每个面都有4个相邻面和一个相对面。然后，通过逻辑推理的方式可以得出结果。

       比如看绿色的面，分别与黑、蓝、红、白相邻，因此相对的就是黄色。再看蓝色，相邻的有黑、绿、黄、白，剩下的红色就是相对面。既然绿与黄，蓝与红分别相对，那么白与黑就相对。

       而如果一开始看黑色，那么只看出绿、蓝与其相邻，得不出结论。因此总结一下这种做法，就是要找到出现次数最多的面，确定其相邻面，然后推导出其相对面。

有了上面的基础，不妨做一下下面的练习：

2. 正方体的展开图

    也从一个简单的问题开始：

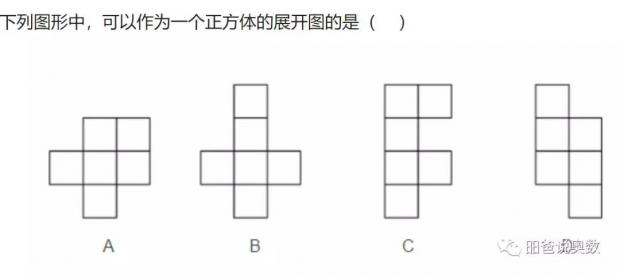
       一个正方体的顶点和三条棱相连，所以展开图中的一个顶点最多只和三条边相连，所以正方体展开图中不可能出现“田”字格，A、D排除。而对于C，最右边的两个正方形重叠了。因此，只有B是正确的展开图。

       一个随之而来的问题是：正方体有多少种不同构的展开图？

       这个问题难度其实很高。网上有各种口诀记忆法，譬如：中间四个面，上下各一面；中间三个面，一二隔河见；中间两个面，楼梯天天见；中间没有面，三三连一线。

       但是，口诀只是在理解后用于辅助记忆的，让孩子自己能探索出所有的展开图才是最有意义的，这需要非常强的有序思维和空间思维作为支撑。

       怎么来思考这个问题，我们得有一个基本的出发点。用展开图中每一行的正方形个数的最大值作为出发点是一个不错的选择。

       不难看出，展开图中处于同一行的正方形个数最大是4。

       （1）6=1+4+1 （表示第一行是1个，第二行是4个，第三行是1个）

       那么第一行的正方形位于最左边，第三行的正方形可以分别位于第三行的4个位置。

       而如果第一行的正方形位于从左至右的第二个位置，那么第三行的正方形可以位于第2，3的位置。有人会问为什么第三行的正方形不能位于最左边和最后边的位置？如果可以，那么把它垂直翻转，就得到了和上面四个展开图中同构的展开图。

       如果第一行的正方形位于从左至右的第3，4个位置呢？那把这个展开图在水平方向翻转，就等同于第一行的正方形位于从左至右的第1，2个位置了，因此也不用再考虑。

       因此，1+4+1型一共就只有下图中的6个。

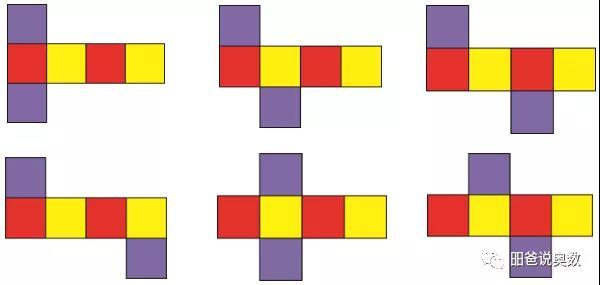
       （2）6=2+4 (表示第一行2个，第二行4个)

       容易发现，这种情况是不可以的，无法构成正方体展开图。

       （3）6=1+1+4

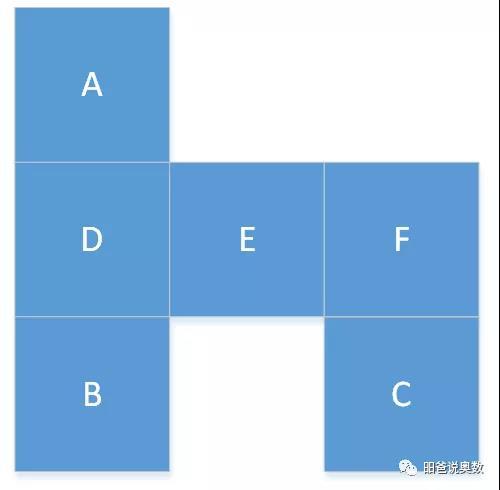
     由于第三行的4个的正方形正好围成正方体的腰，第二行的正方形的正好盖上，第一行的正方形则一定和腰上的某个重叠（比如下图中B和F重叠），无法围成正方体。

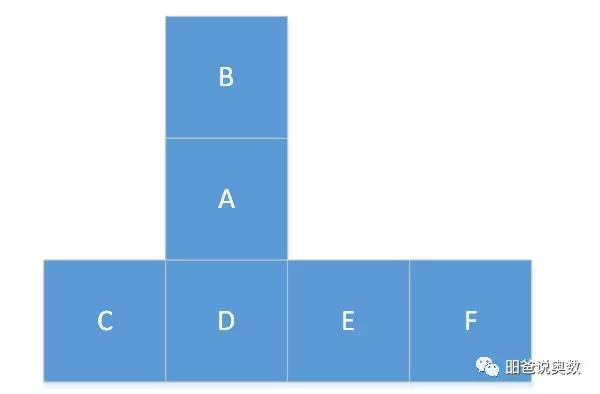
       如果一行的正方形数量最多是3个，那么：

       （4）6=1+3+2 

       首先，展开图不能有田字格。因此第三行的两个正方形只有两种情况，一种是连在一起（但偏在一边），一种是不连在一起。

如果连在一起，那么中间一行的三个正方形围成一个腰还差一个正方形。下面两个正方形一个封底，一个向上翻转合围成一个盛水的容器，最后上面的一个正方形盖盖子。这样得到了下面的三个展开图。

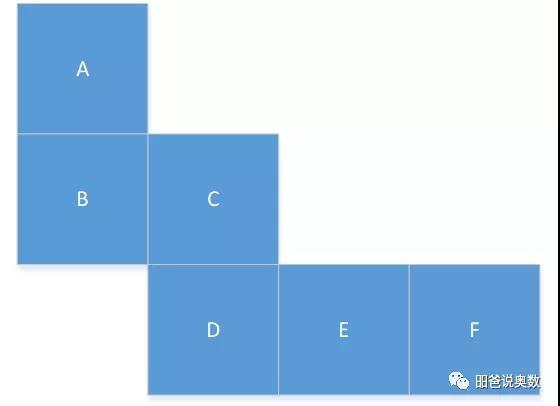
       如果不连在一起，如下面这样，那么第三行的两个正方形就重叠了。也就是说展开图不能出现下面的BCDEF构成的“凹“形。

       （5）6=1+2+3

       譬如这种，也是不行的，折叠后A和F重叠。

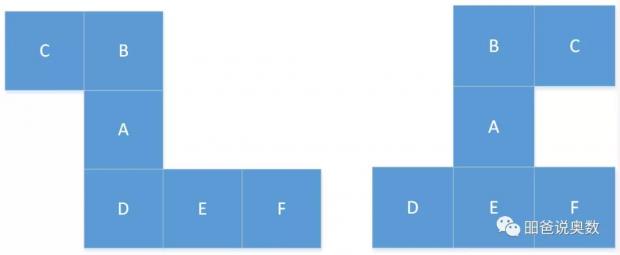
       (6)6 = 2+1+3

譬如下面这两个，也是不行的，有兴趣的可以研究一下哪两个面折叠过程中会重叠在一起。

       （7）6=3+3

由于不能有田字格，又不能有凹形，因此只有下面这一种。

       最后，一行最多有两个正方形

      （8）6=2+2+2

       由于不能有田字格，只能有下面这一种。

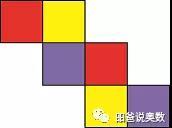
通过上面的分析，可以看出正方体所有不同构的展开图总共有11种，就是上面彩色图给出的。

3. 展开图的相对面

    正方体的相对面，在展开图中分别位于什么位置？这也是一个有趣的问题。

    对于1-4-1型，两个1的必定相对，一行四个正方形间隔的两个也相对，如下（相对面颜色相同）。

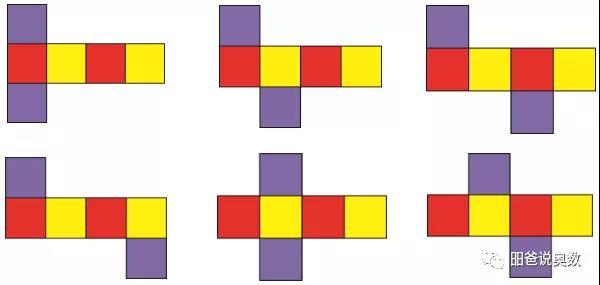
       对于1-3-2型，相对面如下。第二行3个正方形间隔的两个紫色相对，第一行的一个正方形和第三行的最左边的两个分别是容器的盖和底，也相对（黄色），剩下的红色相对。

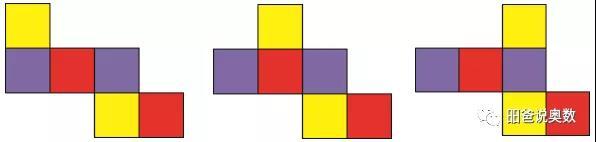
对于3-3型，则根据每行3个的间隔正方形相对即可推导出来。

对于2-2-2型，则相对面如下。

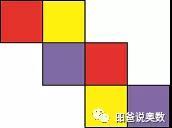
       总结一下，可以发现两个规律：

（1） 直线型的，间隔的正方形是相对面；

（2） 下面这种Z字形状的，Z的起始和结束正方形A,D相对

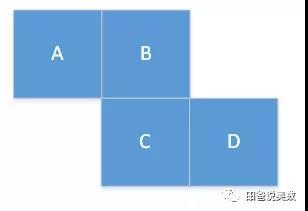
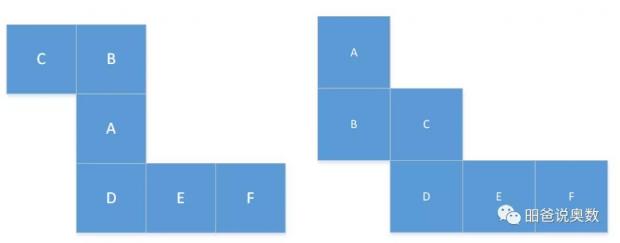
       相对面可以用于分析某个展开图是不是一个合法的展开图。譬如下面两个图形中，左边D和B,F相对，右边D和A,F相对，都违反了只有一个相对面的常识。所以，这两个图都不是合法的展开图。

4. 正方体的旋转

    再来看看美国数学大联盟中的题目：

    Examine the changes in position of thefirst three cubes. Decide how the cube is rotating. Mark the last cube as itshould look to continue the rotation sequence.

    翻译过来就是：观察前三个立方体的旋转变化规律，在最后一个立方体标上合适的数字。

    这个问题实际上涉及到正方体的旋转，仅仅填写数字是是不够的，还需要确定数字的方向。旋转可以沿着三根轴（上下，前后，左右）做顺时针、逆时针旋转。因此一共就有6种不同的旋转方法。比如，上面的例子中，立方体是沿着上下轴做顺时针旋转。

    有兴趣的可以试试下面这个：

       最后，留两个问题供大家思考：

（1） 图⑴是一个正方体的展开图，图⑵的四个正方体中只有一个是和这个展开图对应的，这个正方体是________

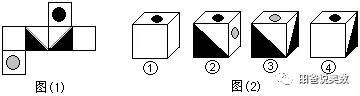
 （2）一只蚂蚁沿着正方体的棱爬行，能否一次不重复地爬完所有的棱？