酷爱数学的拿破仑-昍爸的财新博客-财新网

文 | 昍爸昍妈

一个国家只有数学蓬勃发展，才能展现出它国力的强大。——拿破仑

数学爱好者拿破仑

提起拿破仑，很多人都会对这位军事家的杰出才能啧啧称赞，也有人为他的滑铁卢之败深感惋惜，还有人对他与约瑟芬的旷世爱情唏嘘不已……但鲜为人知的是，拿破仑还是一位极有天赋的数学爱好者，他为法国数学事业的发展做出了巨大贡献。

1797年，年仅28岁的拿破仑从11位候选人中脱颖而出，成为法兰西科学院数学部院士。他对自己能够当选为数学院士感到非常自豪，总是把这个头衔签在他的命令或文告中。

拿破仑曾说：一个国家只有数学蓬勃发展，才能展现出它国力的强大。他认为，人才培养的关键是教育。

1802年至1808年，他颁布了一系列法令，确立了法国精英制大学校的高等教育模式，旨在培养理论联系实际、既有知识又有应用技术的人才。实际上，目前法国最好的两所精英大学——巴黎综合理工学院（École Polytechnique）和巴黎高等师范学校（École normale supérieure de Paris,），就是在拿破仑时代组建的。

我们来看看拿破仑对人才有多重视。1814年，当反法联军兵临城下，法国兵员短缺，有人提议调巴黎理工学校的学生参加战斗时，拿破仑说：“我不愿为取金蛋而杀掉我的老母鸡。”这句名言后来被镌刻在巴黎理工学校梯型大教室的天花板上。

联想到最近任正非的发言，他说：“中国将来要和美国竞赛，唯有提高教育。”而基础教育中，任正非尤其强调数学的重要性。

一位是盛极一时的法兰西帝国的统治者，一位是当今拥有18万员工的中国高科技企业的掌舵人，两者的观点不谋而合——重视教育、重视数学、重视人才，才是立国之本。

巧测莱茵河宽度

1805年，拿破仑率军与普鲁士、俄国联军在莱茵河南北两岸对阵。两军都想向对方阵地开炮，但是，不知宽度的莱茵河成为双方的阻碍，没有精确射程的炮击成了浪费弹药的竞赛。在这种情况下，谁能率先测量出河的宽度，谁就能占得先机。

为了解决这个难题，拿破仑每天远眺莱茵河，在岸边来回踱步。有一次，他偶然发现，对岸的边线（北岸线）恰巧擦着自己戴的军帽的边沿，于是，计上心来。他在这个地点做了一个记号，然后沿着莱茵河的垂直方向一步一步往后退，一直退到莱茵河南岸线也擦着自己军帽沿的地方，停下来又做了个记号。拿破仑让部下丈量出这两个记号之间的距离，并告诉部下：“这就是莱茵河的宽度。”

当天傍晚，法军大炮向对岸敌军阵地射击。炮弹就像长了眼睛般，纷纷飞入敌营。敌军顿时大乱，全线溃败，而法军凭借拿破仑的数学智慧大获全胜。

这则轶事就是理论联系实际在战场上的最佳体现。证明并不复杂，如下图所示，眼睛与帽沿连接成直线。第一次，眼睛、帽沿与河对岸三点一线，即图中所示的BC；第二次，拿破仑后退到D的位置，眼睛、帽沿与法军侧的河岸三点一线，即图中的AD。由于两次的直线平行，构成了平行四边形，因此，莱茵河AB的宽度等于CD的长度。

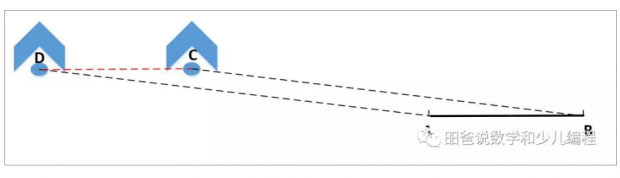
拿破仑定理

上面的例子从侧面说明了拿破仑对几何的敏感度。事实上，拿破仑对几何学有着特别浓厚的兴趣。他在统治法国之前，曾与法国大数学家拉格朗日和拉普拉斯一起讨论过几何问题。

拉格朗日

拿破仑的过人才智和真知灼见令数学家们叹服，以至于他们一起请求：“将军，您来给大家上一次几何课吧!”这样的故事似乎有吹捧夸张之嫌，不过，拿破仑对几何情有独钟是有据可查的。

拿破仑定理是拿破仑在几何学上具有非凡造诣的一个证明。定理是这么说的：以任意三角形的三条边为边，向外构造三个等边三角形，则这三个等边三角形的外接圆中心恰为另一个等边三角形的顶点。该等边三角形称为拿破仑三角形。如下图所示：三角形XYZ是拿破仑三角形。

该定理的证明方法有好多种，都堪称平面几何中的经典证明。有兴趣的读者可以进一步探索。

拿破仑问题

除了上述的例子之外，还有一个据称是拿破仑提出的问题：给定一圆，只用圆规将此圆周四等分。

这个问题最终被解决了，具体解法大概如下：

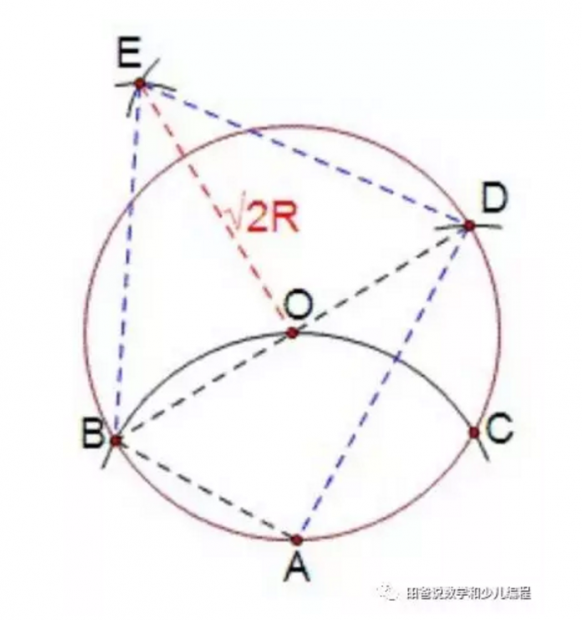
你够格当拿破仑时代的炮兵吗？

拿破仑是炮兵学院出身，在校期间，他专心研究过弹道学，对此很感兴趣。拿破仑的专业技术非常厉害，在他起步的土伦堡战役中，他指挥炮兵部队一打一个准，十分惊人，从此崛起。因此，后来他在军队中积极推广先进的数学方法。从三角函数到微积分方程，拿破仑对炮兵和海军军官工程师提出了很高的要求，以至于拿破仑的大炮打到哪里，工程师的图就画到哪里。

那么，如果一个拿破仑时代的青年想当炮兵军官，他的数学究竟要多好呢？他究竟要学哪一方面的数学，又学到什么样水平和熟练度，才能胜任？

我们不妨来看看拿破仑时代海军与炮兵学院的数学教材。《数学课程（供海军与炮兵使用）》（Cours de mathématiques, à l'usage du corps de l'artillerie）分为六卷本，分别为：

（1）算术。小学水平，部分对数查表除外。

（2）几何。中学水平，包括几何基础、平面三角、球面三角。全等三角形、相似三角形之类是必须掌握的，利用正弦、余弦等定理进行三角测地也是常见例题，以及球面三角公式。

（3）代数。需要掌握如何解一元一次方程、多元一次方程组、一元二次方程，以及它们在几何（尤其是三角）中的初步应用。

（4）、（5）力学、数学、物理。需要掌握微积分基础和中学物理力学。

（6）导航。属于海军范畴，略。

读者朋友，你是否够格当一名拿破仑时代的炮兵呢呢？

话题：