我确信已找到了一个极佳的证明，但书的空白太窄，写不下。

———皮埃尔·德·费马

引 子 

上一篇在北京找人聚会坐车的过程中，想到了聚会的最短路程问题，即：三个人位于北京的不同方位，如何找一个使得三个人跑的总路程最少的聚会地点？

抛开交通工具的便利性和道路的纵横限制，那么这一问题就抽象成：平面上有三个点A,B,C，如何在平面上找一个点P，使得AP+BP+CP之和最小？

这个问题其实有很多不同的应用，比如：

一只猫观察到一老鼠洞共有三个出口，它们不在一条直线上，这只猫应该蹲在何处，才能最省力地顾及到三个出口？

又如：有甲乙丙三个村庄，要在中间建一供水站向三地送水，如何确定供水站的位置以使所需管道总长最小？

“业余数学家” 费马

实际上，这是一个历史名题，有法国著名数学家皮埃尔·德·费马提出。费马正儿八经的职业是律师，他一生从未受过专门的数学教育，数学研究也不过是业余之爱好。但他在数学上的成就不比职业数学家差，被誉为“业余数学家之王”。不过，在17世纪的法国，费马这一业余数学家的成就让其他所有的职业数学家都感到汗颜：他独立于笛卡尔发现了解析几何的基本原理；对于微积分诞生的贡献仅次于牛顿和莱布尼茨，他还是概率论的主要创始人，以及独撑17世纪数论天地的人。著名的费马小定理和费马大定理（又称费马最后定理）都是以费马的名字命名的。

有趣的是，关于费马大定理，费马曾在自己的手迹中写道“我确信已找到了一个极佳的证明，但书的空白太窄，写不下。” 这一“写不下”不打紧，却困惑了世间智者358年。2011年，谷歌（GOOGLE）为了在纪念费玛的诞辰450周年，特地制作了下面的Doodle。

费马点的证明

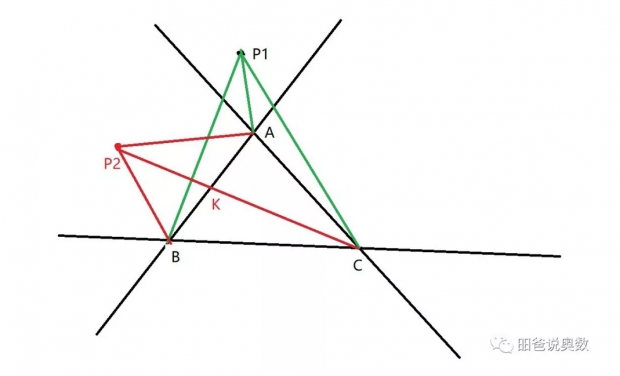
首先，我们证明费马点不可能在三角形的外部。假设费马点在∆ABC的外部，则它必然落在AB, AC, BC延长线构成的六个区域内。假设在P1的位置，则由于∠BAP1+∠CAP1=360°-∠BAC＞180°，故其中必有一个为钝角，不妨假设∠CAP1＞90°，则CP1大于AC，AP1+BP1＞AB，因此AP1+BP1+CP1＞AB+AC，故A点比P1点更合适。

假设在P2的位置，则连接CP2与AB相交于K，则有AP2+BP2+CP2＞AB+CK=AK+BK+CK，因此K点比P2点更合适。

费马点在∆ABC的边界或内部，那么可以采用下面的证明方法。

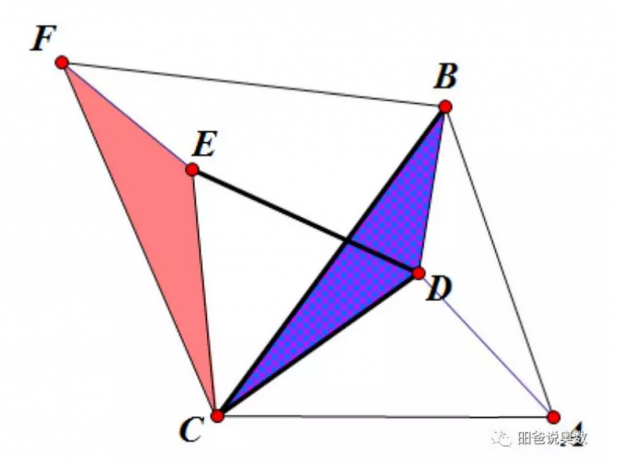
一种证明是用旋转法。如在下图中，将∆CBD绕C点逆时针旋转60度，得到∆CFE。 ∆CDE为正三角形，且BD=EF, 所以AD+CD+BD=AD+DE+EF。当A, D, E, F四点共线时，AD+DE+EF取得最小值，此时∠ADC=180°-∠CDE=120°，∠BDC=∠FEC=180°-∠CED=120°。

因此，D点是使得∠ADC=∠BDC=∠ADB=120°的点。

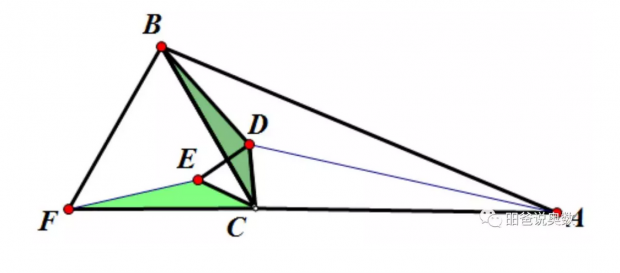
当然，如果∆ABC的某个角本身大于等于120度（假设为∠C≥120°），那么上面这样的内部点是不存在的。此时，费马点就是C点。如下图所示，如果∠C=120°，那么同样，将∆DCB绕C逆时针旋转60°后，AD+CD+BD=AD+DE+EF，当D点与C点重合时取得最小值AC+BC。

除了旋转法，另一种常用的证明方法是面积法。如下图所示，设费马点为P，连接PA, PB, PC，分别过A点作PA的垂线，过B点作垂直于PB的垂线，过C点作垂直于PC的垂线，三条垂线延长交于X,Y,Z。则，易知∆XYZ为正三角形，设其边长为L, 面积为S。根据面积法可知，PA+PB+PC=2S/L。对于任意一点P’，同样作P’A’ ,P’B‘,P’C’分别垂直于XZ, XY, YZ。根据面积法可知P’A’ +P’B‘+P’C’=2S/L，由于P’A≥P’A’, P’B≥P’B’, P’C≥P’C’, 因此P’A’ +P’B‘+P’C’ ≥PA+PB+PC，仅当P’与P点重合时两者相等。

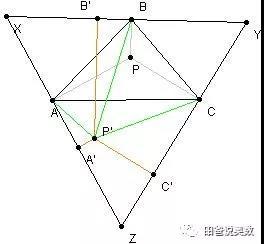
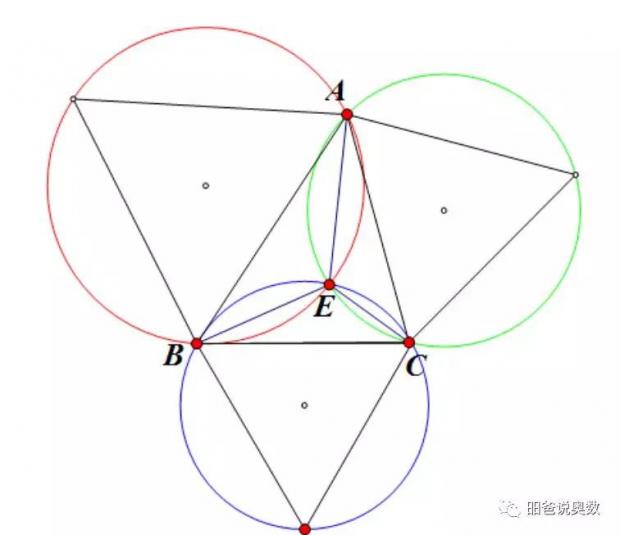
费马点的特征已经知道了，怎么利用尺规作图把费马点确定下来呢？也很简单，以AB, AC, BC分别为边向外做正三角形，分别得到三个三角形的中心，分别作三个三角形的外接圆，其交点即为费马点，如下图所示。

最后，留一道题供读者思考。

据史料记载，费马曾思考过这样一道数学题。古希腊亚历山里亚城里有一位久负盛名的学者，名叫海伦。有一天，有位将军不远千里专程前来向海伦求教一个百思不得其解的问题：将军从甲地出发到河边饮马，然后再到乙地军营视察，显然有许多走法。问走什么样的路线最短呢？