我们的教育缺乏对失败的容忍-昍爸的财新博客-财新网

当你把所有的错误都关在门外，真理也就被拒绝了——泰戈尔

失败是成功之母

我们从小就被反复教育：失败是成功之母。但试问：我们如今的基础教育，有多少时间和空间允许孩子失败？

不妨让我们来深入剖析一下这句人人皆知的名言的内涵。

第一层含义：要允许失败，没有失败就没有成功。

但这，还远不够，失败不会无缘地导致成功。这也就有了我们的第二层含义：失败从来不会无缘无故导致成功。需要在失败中总结经验，获得走向成功的启示。

再来看看我们的学校和家长的教育：这个题目都讲过多少次了，怎么还错？再错，罚做10题。

这，不应该是失败走向成功的正确之道。我理解的失败，应该重点是自我探索的失败，在曲折中前行，直至成功。失败和成功，是两条路。你不走，怎么知道哪一条是死路？

再来看看前些年风靡全国的小学华罗庚金杯赛。60分钟答10道题。如此短暂的时间，考生哪有试错的时间？假如两个考生，一个经过训练，一个没有，最后分别考了80分和30分，孰优孰劣？我觉得很难说。

反而是我们最高级别的CMO选拔赛，半天时间考3道题，两个半天一共考6道题，让考生有充分的时间去探索解答。

标准答案之伤

我们的试题，总是讲究标准答案。有些考题出来了，明明是因为出题人的不慎导致理解的多样性，但依然没办法，总还得有个标准答案。比如：最少要用多少个同样大小的正方体，才能使得从正面、上面、右面看都是一个2×2的正方形？

孩子在做的时候就会有疑问。这取决于前提假设：你是在地球上还是在太空失重环境？即便在地球，允许不允许用一些额外的手段让正方体漂浮，比如充满氢气可以悬浮在空中的正方体？

语文的阅读理解更是如此。有些文章本就是不同心境的人读有不同的理解，可也得搞出标准答案。那是不是也可以为蒙娜丽莎的微笑出一道选择题：

请问蒙娜丽莎的微笑是？（）

A 快乐的笑；B 苦笑；C 傻笑；D 俏皮的笑

有些事情本来就是千人千面，可我们的教育一定得搞成千篇一律。

我们需要培养什么样的人？

建国之初，我们国家一穷二白，百废待兴。彼时我们的人才培养需求是如何快速培养出大批熟练的技术工人，让我们能短期内从一个农业国变成一个工业国。

而今，我国已经是一个工业大国。现正面临产业升级换代困难、基础创新不足的局面。如果还是以培养技术工人的思路来培养学生，那么基础教育和国家的需求显然是背离的。基础原创性的突破要求我们转变我们的教育模式。

我们现今的中小学培养，基本还是延续了流水线工人的培养模式，即培养了大批会快速解答固定题型的学生。离开了这个流水线，换了没见过的题型，他就什么不会了。

教育，本应该教会思考，而不是扼杀思考。学会独立思考，正是做出原创性成果所必备的素质，也是我们当前教育的短板。思考是一件奢侈的事，需要足够的时间和空间。而这些，恰恰是我们没有耐心和条件给孩子的。除却学校教育，许多孩子的周末课外班都满档，一场赶一场，家长和孩子都疲于奔命，哪还有时间静静地思考?

有些人会说，原创性工作是少数人的事，大部分人都不需要思考。没错，但楼阁从来都不能凭空而建。没有坚实的金字塔塔基，塔尖就不复存在。否则，你凭什么要求没有全国没有足球氛围的中国队进入世界杯决赛圈？

剧场效应与基础教育的悲剧

剧场效应( theatre effect ），在经济学中是指：如果剧院着火了，按照个人利益最大化，那就是先跑出去，如果每个人都这么想这么做，其结果必然是大家都拥堵在门口，谁都跑不出去，个人追求利益最大化而不考虑他人利益的行为，导致了群体悲剧的上演。

这一人人都懂的道理，却成了人人都跨不过去的坎。剧场悲剧，每日都在上演，剥夺了孩子们的思考时间和试错空间。结果是，我们用大量的金钱、时间、人力堆积起了巨额的教育GDP，却培养了一大批不会独立思考的学生。

从一道数学题谈谈如何独立思考

期末考试有5道题，答对3道题及以上才算及格。有100人参加考试，答对第一题的有81人，答对第二题的有91人，答对第三题的有85人，答对第四题的有79人，答对第五题的有74人，请问，在这次考试中至少有多少人及格？

不少学过一点奥数的同学，一开始会把这一问题和容斥原理关联起来。假设做对1，2，3，4，5题的分别是A、B、C、D、E人。但后面的问题来了：要求的集合如何表示？大家学过的容斥原理，一般3个是极限（当然，到大学里会拓展到n个集合）。另外，五个集合的并是多少？任何几个集合的交集又是多少？这些都是不确定的。

但依然会有不少学了容斥原理的学生一头扑在里面，一旦碰壁，便不知所措。因为，他不会从原点开始思考。

反而是没有经过训练的学生，会对这个题有一点直觉的感受。

思考从这里开始：怎样才能让及格的人少？

一个初级的想法是让及格的人答对的题尽量多，比如5题全答对。

第一个想法，5题都对最多有74个人。第一步，可以画出下面的图。但在这个图里，还有一些人是4题都对，有一些人3题都对，他们也都是及格的。但还有一些人只对1题或0题。在第一次画出的图中，有81人及格。我们可以通过微调，比如让做对第3题的7个人换成后面的7个人，把做对第4题的5个人也换成后面的5个人（图中①，②所示）。这样，除了74个5题全对的，后面的26人最多只做对2题，因此都不及格。

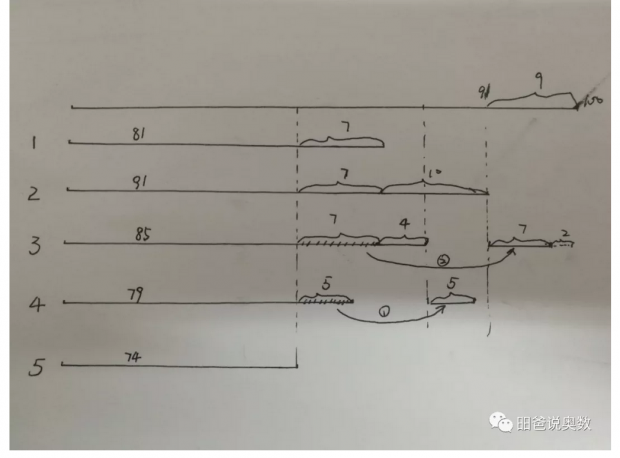
但问题是，能不能让更多的人不及格呢？细心的同学可能已经发现，即便做了上面的调整，后面还有一些人1道题都没做对或者只做对了1道题。如果我们把前面74人中的最后一个5题全对的人，令其第3，4，5题做错，将做对这题的人分别调整到第99人、第99人和第100人。那么及格的人又少了一个（第74个人此时只做对1，2题，不及格）。当然，这样的调整还可以继续。

那直到什么时候为止呢？其实主要看后面。如果前面及格的变成了不及格，而调整到后面不及格又变成了及格，那么这样的调整是无益的。我们希望做的调整是让前面的人变成不及格，而后面的不及格人的状态维持不变。比如，如果前面某人做对了3题，后面某人做对了1题，那么把前面这人做对的其中1题让后面的人做对，则两人都做对2题，及格的人数就少1人。

不及格状态每个人能做对的题量最多是2题，我们希望这些错题集中分布在这群不及格人身上，还得要求这群人的人数最多，从而及格的人数最少。这其实引申出了两种思考途径。

途径1：最后的最佳状态是及格的人5题都对，不及格的人都做错2题。

按照这一思路，假设及格的人为x人，那么有：x×5+(100-x)×2=410, 恰好x=70。

这一答案表示70个人做对了5道题，剩下的30人做对了60道题，每人恰好做对2道题。能不能实现这一点，我们可以比较容易地构造出一种方案，如下图所示（70故意画的短一点）。

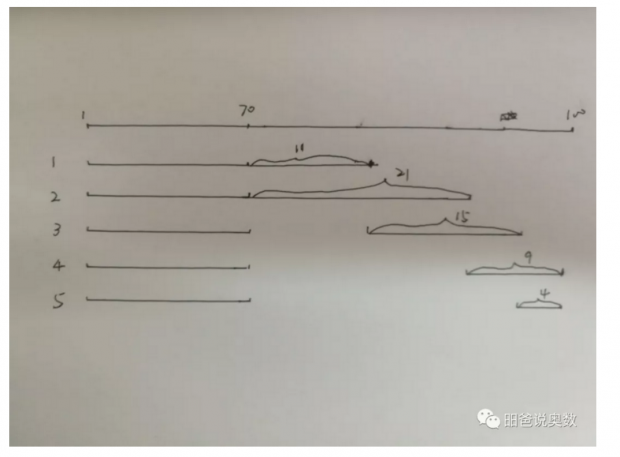
途径2：不及格的人数应该最多。

实际上，100个人一共做错了90道题次。不及格至少要错3题，所以，最多只有90÷3=30人不及格。因此及格的人最少有70人，同样可以给出构造方案。

有些接受过训练同学的一开始就告诉我说：及格的人数最少，就等价于不及格的人数最多。没错，这是一种逆向思维。但这种逆向思维并非一开始就可以蹦出来的。通过分析，则可以水到渠成得到这一结论。

同样是这一题，稍微改一下：

期末考试有5道题，答对3道题及以上才算及格。有100人参加考试，答对第一题的有81人，答对第二题的有91人，答对第三题的有85人，答对第四题的有79人，答对第五题的有74人，请问，在这次考试中最多有多少人及格？

好了，如果受过训练，一上来就逆向思维。最多多少人及格，等价于最少多少人不及格。错题总数是90题，要不及格的人数最少，那么应该让每个人错的题最多，即每人错5题，因此最少90÷5=18人不及格，从而最多有100-18=82人及格。

乍一看，好像还有那么点道理。但实际上，这是惯性思维在作怪。错题总数是90题，分明可以分布到不同的人身上。极端一点，一个人错90题，其余人不错（当然，在这个题里，这个极端假设是不可能达到）。但这也从侧面说明，及格的人应该可以很多，基本上可以让所有人都及格。

这不，下面的构造方法就可以。如何构造本身就是试错纠正的过程。很少有人能一步成功。在下面的构造过程中，一开始后面的一部分人只对了两题，属于不及格，可以随便移动一部分到最后（比如途中将做对第3题的26-40这15个人移动到最后），那么所有的人都做对3题以上，也就是都及格了。

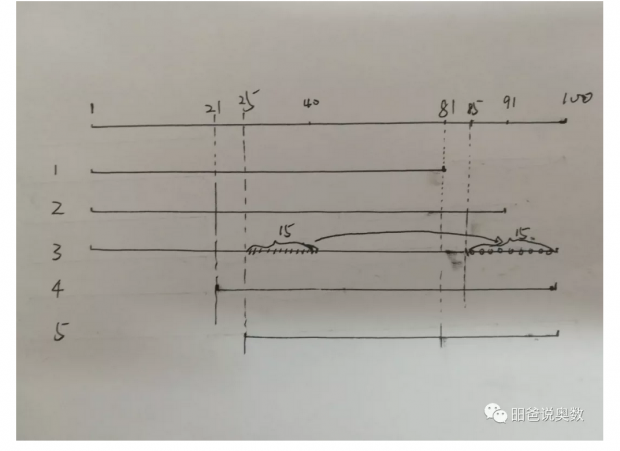
话题：