神奇的斐波那契数列——大自然的数学密码-昍爸的财新博客-财新网

我们固然不能说，但凡合理的都是美的；但凡是美的确实都是合理的，至少应该是合理的。——歌德

最近手机的锁屏被自动设置为下面这副图，注释为：螺旋即是无限。

从爬楼梯开始

暑假，昍的编程小老师给他们出了道爬楼梯的题：

假设有10级楼梯，一步可以跨1级2级楼梯，请问爬完10级楼梯一共有多少种不同的爬法？

这个题目乍一看，并不简单。昍一开始也没头绪，我给了他一点启发：10级楼梯太多，先从少一点楼梯级数开始试试。

1级楼梯：1种

2级楼梯：2种

3级楼梯：3种

4级楼梯：5种

5级楼梯：8种

这之后，一般的小朋友都可以找出规律，6级楼梯13种。

但这还仅仅是一种合理的猜测，为什么是正确的呢？

不妨这么思考，比如5级楼梯，第一步可以怎么走呢？可以有两种走法：一种是跨1级楼梯，那还剩下4级楼梯，有5种走法；另一种是跨2级楼梯，则剩下3级楼梯，有3种走法。根据加法原理，那么5级楼梯一共有5+3=8种爬法。

推广一下，假设n级楼梯的爬法为f(n)种，那么第一步可以跨1级楼梯，剩下n-1级楼梯，有f(n-1)种爬法，第一步也可以跨2级楼梯，剩下n-2级楼梯，有f(n-2)种爬法，因此f(n)=f(n-1)+f(n-2)。这就是斐波那契数列的递推关系。

当然，就这一题本身，还有不同的解法。没有想到递归，很多人可能会将这一问题转换为：有多少种不同的1和2的有序组合，使得其相加之和为10？

可以这么来解这个问题：

有序组中包含10个元素，即不包含2：1种（10个1）

有序组中包含9个元素，1个2和8个1：9种（2出现在9个位置中的任何一个）

有序组中包含8个元素，2个2和6个1：28种（8个位置选2个位置放2）

有序组中包含7个元素，3个2和4个1：35种（7个位置选3个位置放2）

有序组中包含6个元素，4个2和2个1：15种（6个位置选2个位置放1）

有序组中包含5个元素，5个2：1种

总计：1+9+28+35+15+1=89种，与斐波那契递推得到的答案一致。

但这种解法的问题在于其扩展性差。问题存在于下面两方面：

如果是100级楼梯而非10级楼梯，那么上面的分析数量就会大幅增加；

如果每一步可以跨的级数增加，例如可以跨1级、2级、3级，那么上面的分析复杂度将呈几何级数增长，而如果采用递推分析法，则很简单，就是：f(n)=f(n-1)+f(n-1)+f(n-3)。

斐波那契数列的来由

斐波那契序列在公元前的印度就已经被提出，在欧洲由公元十二世纪的意大利数学家莱昂纳多·斐波那契以兔子繁殖为例子引入，因此又称为“兔子数列”。

假如兔子在出生两个月后就有繁殖能力，一对兔子每个月能生出一对小兔来，如果所有兔子都不会死，那么12个月后一共有多少对兔子？

这一问题可以通过下面的图形象地予以表述。

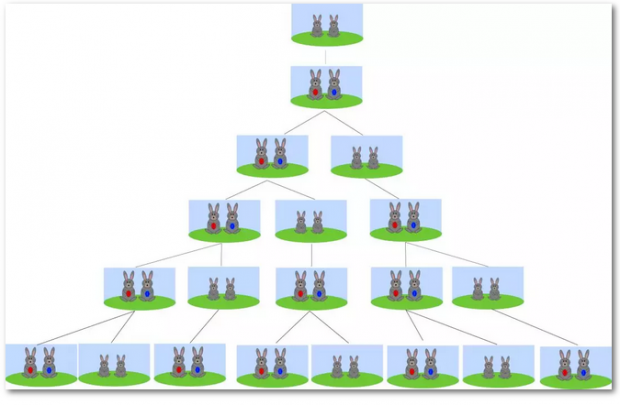
斐波那契数列在自然科学的其他分支，有许多应用。例如，树木的生长，由于新生的枝条，往往需要一段“休息”时间，供自身生长，而后才能萌发新枝。所以，一株树苗在一段间隔，例如一年，以后长出一条新枝；第二年新枝“休息”，老枝依旧萌发；此后，老枝与“休息”过一年的枝同时萌发，当年生的新枝则次年“休息”。这样，一株树木各个年份的枝桠数，便构成斐波那契数列。这个规律，就是生物学上著名的“鲁德维格定律”。

斐波那契数列与黄金分割

斐波那契数列的有趣之处在于它的通项公式：

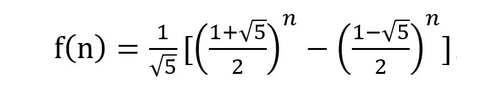
一个整数序列，通项公式竟然用无理数表达。更重要的是，这个无理数，很特别！

斐波那契数列的前一项和后一项之比无限接近一个数：黄金分割，即0.618。不信可以试几个： 1÷1=1, 1÷2=0.5, 2÷3=0.666..., 3÷5=0.6, 5÷8=0.625， 55÷89=0.617977…， 144÷233=0.618025…，46368÷75025=0.6180339886。这个极限可以用数学的方法证明，在此略去。

公元前4世纪，古希腊数学家欧多克索斯第一个系统研究了黄金分割的问题，并建立起比例理论。他认为所谓黄金分割，指的是把长为L的线段分为两部分，使其中一部分对于全部之比，等于另一部分对于该部分之比。而计算黄金分割最简单的方法，即是计算斐波那契数列1，1，2，3，5，8，13，21，...第二位起相邻两数之比。

人们发现，按0.618:1来设计的比例，画出的画最优美，在达·芬奇的作品《蒙娜丽莎》和《最后的晚餐》中都运用了黄金分割。而现今的女性，腰身以下的长度平均只占身高的0.58，因此古希腊的著名雕像断臂维纳斯及太阳神阿波罗都通过故意延长双腿，使之与身高的比值为0.618。建筑师们对数字0.618特别偏爱，无论是古埃及的金字塔，还是巴黎的圣母院，或者是近世纪的法国埃菲尔铁塔，希腊雅典的巴特农神庙，都有黄金分割的足迹。

如果我们把斐波那契数列作为一个个正方形的边长，按照下图的方式拼起来，并按照图示方式画出曲线，那就得到了“斐波那契螺旋”，这一螺旋是黄金螺旋的最佳近似。

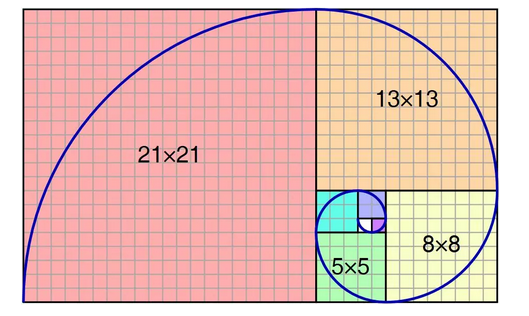
神奇的是，大自然中，小到动植物，大到星云，都呈现出这一螺旋。这一神秘的数字，把看似毫不相干的大自然完美地串在了一起。

话题：