第一是数学，第二是数学，第三是数学。 

—— 伦琴

数字2和3有什么奥妙？相信稍微学过点数学的人都能道出个一二三。比如：2是偶数和唯一的偶质数，3是最小的奇质数，能被3整除的数的特征是所有位之和能被3整除(慢着，why?)。

找次品问题

当然，这不是2和3的全部。且看老王在群里抛出的某思题目和解答。题目如下：

18个球，外观一模一样，其中有一个球比其它球轻，仅使用一架天平，请问最少称几次能找出轻的球？

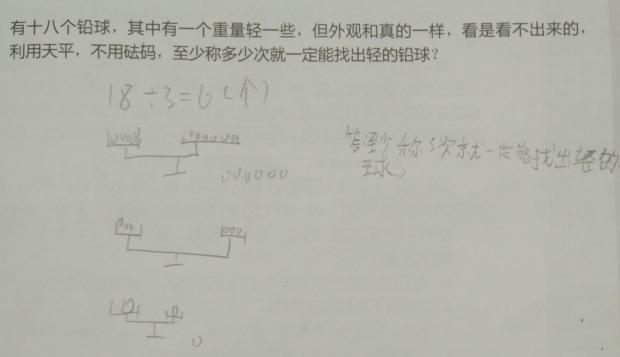
老王家二年级小朋友给出的答案如上图所示，大意是把18个球6个一组分为A、B和C三组，任意选择两组(如A, B)称一下。如果天平是平的，则表示轻的球在C这一组；如果天平不平（假设A重于B），则表示轻的球在B这一组。

接着选择轻球所在的组，将球3个一组分为2组，放天平两端称一下，则天平一定不平且所找的球一定在轻的一端。于是再在这一组3个球中任取两个球称一下，如果天平平衡，则剩下的那个球是便是要找的球，否则，天平两端轻的那个就是要找的球。

这个答案无懈可击，但有一点孩子可能并不理解：第一次把18个球分为3组，第二次把6个球分为2组，第三次把3个球分为3组。什么时候该把球分为3组，什么时候分为2组，有什么讲究？我相信某思并未给出说明。

后来老王又给了一个续集，就是6个球怎么找，相当于原来问题的子问题。但是，如果球的数目不是3的倍数呢？昍爸前面推崇的举一反三，就是要通过反三能够解决一类问题，而不是特殊问题。

晚上和昍探讨这个问题，没有球，就用樱桃来玩这个游戏。本来孩子对做数学题已经有抵制情绪，一听说是玩游戏，他突然又兴致高涨。

一直以来，昍爸都喜欢从易到难，让孩子在实践中自己逐步找到解决问题的方法。

先从2个樱桃开始，很简单1次就够。

接着是3个樱桃。第一次碰到这样的问题，孩子一开始说要2次（拿一个和另外两个分别称一次）。我引导他思考有没有更少的方法，这个比较简单，他很快就明白如果天平是平的话，那剩下的一个就是轻的，无需再称。

下面是4个樱桃，2个一组分2组，称一下找出轻的一组，然后回到两个樱桃的情形，因此一共两次。

5个樱桃，他的做法是分成3组<1, 2, 2> ，先将2个一组的称一下就可以。当然也可以分成2组<2, 3>，先将第一组的两个放天平两端称一下，若不平，则找到答案；若平，则轻的在3个那组里，回到前面3个樱桃的情形，再用一次即可。

6个樱桃，按老王家小朋友的做法，可以3个一组分成2组。昍的做法是分成2个一组3组，先把两组称一下，若天平平衡，则轻的在剩下那组里，否则轻的在天平轻的一端。于是问题再次回到2个樱桃的情形。

7个樱桃，一番简单琢磨，分为<2，2，3>三组，先将前两组称一下，若平衡，则轻的在3个樱桃一组，回到3个樱桃的情形，若不平衡，则回到2个樱桃的情形，均仅需再用一次即可，因此7个樱桃需2次。

沿着这一思路，8个樱桃分为<2，3，3>三组，9个樱桃分为<3，3，3>三组，10个樱桃分为<3，3，4>三组，11个樱桃分为<3，4，4>三组，12个樱桃分为<4，4，4>三组，13个樱桃分为<4，4，5>三组。

玩到13个，孩子没有兴趣了。他基本上知道对于任意数目的樱桃，可以大致均分为3组，取两组同样多的先称一次。如果天平平衡，则轻的就在剩下的那组里，而剩下的那组之前已经知道最少称多少次；如果天平不平衡，则轻的在天平较轻的一端，也可以利用之前的结论。这，不就蕴含了朴素的递归思想和计算机算法里的分治与动态规划吗？

当然，还有一个问题，任意数目的樱桃是否一定可以分为差不多的3组呢？怎么分？二年级正好在学带余数的除法。作业本上经常有这类题目：

□÷○=△…5，请问○最小是多少？

□÷○=△…2，请问□最小是多少？

上面讲樱桃分为3组的问题，不正可以表示成下面这样的带余数除法吗？

□÷3=△…○

其中○可以是0，1或2。

l  若○=0，则正好分为<△,△,△>三组；

l  若○=1，则正好分为<△,△,△+1>三组；

l  若○=2，则正好分为<△,△+1,△+1>三组。

所以，无论是多少个樱桃，都可以正好分为三组，且其中一定有两组数目一样多，可以先称一次。

当然，从数学的角度，可以进一步探寻任意数目的球至少需要多少次称法的一般性结论。为此，我给孩子列出了下面的表格：

可以看到，3个球，9个球和27个球之后，称的次数要增加1，而3，9，27有什么规律呢？简单观察就知道它们正好是3¹, 3², 3³。故对任意一个数N，我们假设3^kk+1，那么至少需要称k+1次。进一步地，k可以用N表示成中学以后引入的对数表示。

为什么每次分为3份可以得到最少的称数呢？每次分成两份（也即2分法），也能找出次品，每称一次将问题规模缩减为原来的二分之一；但每次分成3份，借助于天平和球已知轻（或重）的知识，每称一次可以将问题的规模缩减为原来的三分之一。

自然数拆分问题

上面这题目让我联想到了之前群里的另一道题：一个自然数可以拆分成若干个自然数的和，这些拆分后的自然数的乘积最大值是多少？

比如说11=2+2+2+5，那么对应的乘积为2×2×2×5=40。这当然不是最佳的拆分法，换一种11=2+3+3+3，对应的乘积为2×3×3×3=54。

到底如何拆分才能使得乘积最大，经过一番观察和尝试，我们首先有下面的结论。

结论一：如果拆分后有某个拆分数大于等于4，那么将它进一步拆成两个数（每个数至少为2）后，乘积一定大于等于原来的拆分数乘积。

比如5=2+3，8=3+5。事实上，若a=b+c (设b>=c)，有b×c>=b+c对任意的c>=2都成立，当a=4时等号成立。

此外，还有另一个显然的结论。

结论二：对任意一种拆分法，为了使得拆分数的乘积最大，拆分数不应该包含1。

这是因为：a=(a-1)+1>(a-1)×1，与其拆了，还不如不拆。

那么，对于任意自然数，怎么拆才能保证乘积最大？很简单，只要拆分数大于3，那就按上面的规则继续拆吧，新乘积一定大于等于原来的乘积。

所以，乘积最大的拆分法一定是将这个自然数分成若干个3和2（当然也可以是4，姑且假设我们把4都拆分成2+2）的和。

最后，再来看看是拆分成3划算还是2划算？

简单的尝试就可以看出所以然：6=3+3=2+2+2， 但3²>2³，因此和相等时，拆分成3的乘积要大于分解成2的乘积。

最后，还是以一个球找次品的问题结束本篇，但难度和前面显然不是一个档次。据说这是微软的一道面试题，有兴趣的家长朋友可以挑战一下：

12个球外观一样，其中有一个球与其它球重量不一样，仅用一架天平，请问最少需要几次才能确保找出这个不一样的球？

长按关注昍爸说奥数公众号！